| \(0 < e^x\) | \(e^1 = 0\) | \(e^{ln(x)} = x\) |
| \(ln(e^x)=x\) | \(e^x * e^y = e^{x+y}\) | \((e^x)^n = e^{xn}\) |
| \(\frac{e^x}{e^y}= e^{x-y}\) | \(e^{-x}=\frac{1}{e^x}\) |
Bijective/Injective/Surjective
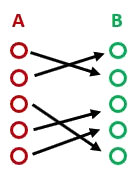
Injective
Chaque membre de A a 1 seule correspondance en B
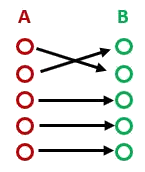
Surjective
Chaque membre de B a au moins 1 correspondance en A
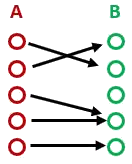
Bijective
Injective & Surjective :
Chaque membre de A a 1 seule correspondance en B
Chaque membre de B a 1 seule correspondance en A