Les limites sont un concept fondamental en mathématiques qui permet de décrire comment une fonction se comporte à l’approche d’un certain point. Elles permettent de déterminer les valeurs approchées auxquelles une fonction tend lorsque la variable indépendante se rapproche d’une certaine valeur, même si la fonction n’atteint jamais cette valeur. Les limites sont utilisées pour étudier la continuité, les dérivées et les intégrales d’une fonction. Les limites peuvent être finies ou infinies, et il est souvent possible de les calculer en utilisant des règles de calcul de limites standard. Les limites sont également utilisées pour étudier les comportements à l’infini des fonctions, comme les asymptotes.
Les limites sont une partie importante des études mathématiques avancées, et peuvent être utilisées pour résoudre des problèmes dans de nombreux domaines, tels que la physique, la chimie, la finance et l’ingénierie.
$$\lim_{x \to +\infty} x = +\infty$$ $$\lim_{x \to +\infty} e^x = +\infty$$ $$\lim_{x \to +\infty} ln(x) = +\infty$$ $$\lim_{x \to +\infty} x^n = +\infty (n \in \mathbb{N})$$ $$\lim_{x \to -\infty} x = -\infty$$ $$\lim_{x \to -\infty} e^x = 0+$$ $$\lim_{\begin{array}{cc} x \to 0 \\ x >0 \end{array}} ln(x) = -\infty$$ $$\lim_{x \to -\infty} x^n = +\infty \text{ si n pair ou} -\infty \text{ si n impair}$$
Additions des limites
Multiplication des limites
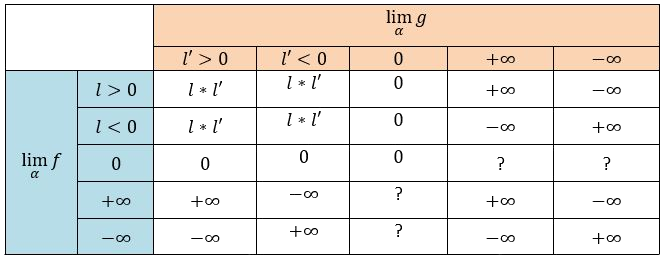
Inversion des limites
Limite à l’infini d’un polynôme
Limite à l’infini du terme du + haut degré, exemple :
$$\lim_{x \to +\infty} x^3-x^2+5x-1 = \lim_{x \to +\infty} x^3 = +\infty$$
Limite à l’infini d’une fraction rationnelle
Limite à l’infini du quotient du terme de + haut degré du numérateur par celui du dénominateur, exemple :
$$\lim_{x \to +\infty} \frac{-x^2+5x-1}{2-3x} = \lim_{x \to +\infty} \frac{-x^2}{-3x} = \lim_{x \to +\infty} \frac{x}{3} = +\infty$$
$$\lim_{x \to +\infty} \frac{e^x}{x^\alpha}= +\infty (\alpha \in \mathbb{R})$$
$$\lim_{x \to -\infty} x^ne^x = 0 (n \in \mathbb{z})$$
$$\lim_{x \to +\infty} \frac{ln(x)}{x} = 0+$$
$$\lim_{\begin{array}{cc} x \to 0 \\ x >0 \end{array}} x.ln(x) = 0-$$
Limites nulles et limites en 0:
$$\lim_{x \to \alpha} f(x)=l \Longleftrightarrow \lim_{x \to \alpha} (f(x)-l)=0$$
Théorème (Règles) de comparaison
On suppose :
$$\forall x f(x) \leq g(x)\text{ et que }\lim_{x \to \alpha} f(x)\text{ et }\lim_{x \to \alpha} g(x)\text{ existent (limites finies ou infinies)}$$
Alors:
$$\lim_{x \to \alpha} f(x) \leq \lim_{x \to \alpha} g(x)$$
$$\text{Si } f(x) < g(x)\text{ alors }\lim_{x \to \alpha} f(x) \leq g(x)$$
On suppose que les 2 limites existent, mais possible qu’une ou aucune des limites existent même si \(f(x) \leq g(x)\) , ce qui amène à :
Théorème des gendarmes
Soient \(f\),\(g\) et \(h\) 3 fonctions. On suppose que : \(\forall x f(x) \leq g(x) \leq h(x)\)
On suppose aussi que :
$$\lim_{x \to \alpha} f(x)\text{ et }\lim_{x \to \alpha} h(x)\text{ existent et sont égales : }\lim_{x \to \alpha} f(x)=\lim_{x \to \alpha} h(x)=l$$
Conclusion : La limite de \(g(x)\) existe quand \(x \rightarrow \alpha\), et:
$$\lim_{x \to \alpha} g(x)=l$$
Application :
$$\text{Soit }\lim_{x \to \alpha} g(x)=0\text{ et }\forall x \mid f(x)\mid \leq g(x)$$
Conclusion :
$$\lim_{x \to \alpha} f(x)=0$$
Cas particulier :
$$\text{Soit }\lim_{x \to \alpha} f(x)=+\infty \text{ et }\forall x f(x) \leq g(x)$$
Donc:
$$\lim_{x \to \alpha} g(x)=+\infty$$
\(\rightarrow\) Pour \(lim=+\infty\), 1 seul gendarme est suffisant comme pour \(-\infty\)
Composition de limites
$$\lim_{x \to \alpha} f(x)= \beta \text{ et } \lim_{x \to \alpha} g(x)=\gamma \rightarrow \lim_{x \to \alpha} g \circ f(x)=\gamma$$
Ou :
$$\lim_{x \to \alpha} f(x)= \beta \text{ et } \lim_{x \to \alpha} g(y)=\gamma \rightarrow \lim_{x \to \alpha} g(f(x))=\gamma$$
Exemple
Calculer:
$$\lim_{x \to \alpha} \frac{(ln(x))^\alpha}{x^\beta } avec \alpha>0 et \beta>0 et x>0$$
Dénominateur : \(x^\alpha = e^{\beta ln(x)} \rightarrow ln(x^n ) = n.ln(x)\)
$$\Longrightarrow \lim_{x \to +\infty} ln(x) = +\infty; \lim_{x \to +\infty} \beta.ln(x) = +\infty\text{ car }\beta>0 $$
$$\lim_{x \to +\infty} e^x = +\infty$$
Donc:
$$\lim_{x \to +\infty} e^{\beta lnx} = \lim_{x \to +\infty} x^\beta = +\infty$$
Numérateur :
$$\lim_{x \to +\infty} ln(x) =+\infty; \lim_{x \to +\infty} y^\alpha = +\infty;\text{ donc }\lim_{x \to +\infty} (ln(x))^\alpha = +\infty$$
Forme indéterminée : \(\frac{\infty}{\infty}\)
Exemple d’étude de limite
Soit:
$$f(x)=\frac{(ln(x))^\alpha}{x^\beta } =(\frac{ln(x)}{x^{\frac{\beta}{\alpha}}})^\alpha$$
$$ g(x)=\frac{ln(x^1)}{x^{\frac{\beta}{\alpha}}}=\frac{ln(x^{\frac{\beta}{\alpha}.\frac{\alpha}{\beta}})}{x^{\frac{\beta}{\alpha}}}=\frac{ln((x^{\frac{\beta}{\alpha}})^{\frac{\alpha}{\beta}})}{x^{\frac{\beta}{\alpha}}}=\frac{\alpha}{\beta}.\frac{ln(x^{\frac{\beta}{\alpha}})}{x^{\frac{\beta}{\alpha}}}$$
Limite en \(+\infty\) :
$$g(x)=\frac{ln(x)}{x^{\frac{\beta}{\alpha}}}$$
$$\lim_{x \to +\infty} x^{\frac{\beta}{\alpha}}=+\infty\text{ et }\lim_{y \to +\infty} \frac{ln(y)}{y}=0+\text{ (forme indéterminée de référence)}$$
$$\lim_{x \to +\infty} \frac{ln(x^{\frac{\beta}{\alpha}})}{x^{\frac{\beta}{\alpha}}}=0+$$
Multiplication par \(\frac{\beta}{\alpha}>0\):
$$\lim_{x \to +\infty} g(x)=0+$$
On remarque :
$$f(x)=g(x)^{\alpha} \rightarrow\text{ Limite en 0+ de }x^{\alpha}=e^{\alpha .ln(x)}?$$
$$\lim_{x \to 0+}ln(x)=-\infty\text{ donc }\lim_{x \to 0+} \alpha.ln(x)=-\infty (\alpha>0), \lim_{y \to -\infty} e^{y} =0+$$
Donc: $$\lim_{x \to 0+} e^{\alpha .ln(x)}=\lim_{x \to 0+} x^{\alpha }=0+$$
Conclusion :
$$\lim_{x \to +\infty} g(x)=0+\text{ et }\lim_{x \to 0+} y^{\alpha}=0+,\text{ donc }\lim_{x \to +\infty} f(x)=\lim_{x \to +\infty} g(x)^{\alpha}=0+$$
Donc:
$$\forall \alpha>0, \forall \beta>0, \lim_{x \to +\infty} \frac{ln(x)^{\alpha}}{x^{\beta }}=0+$$
Les fonctions puissances « l’emportent » sur les fonctions logarithmes.