Study Plan
Let \(f\) : (domain of definition \(x\), e.g.: \(\mathbb{R}\)) \(\rightarrow\) (domain of definition \(y\), e.g.: \(\mathbb{R}\)), \(f(x)=\) …
- Specify definition set
- Detect & investigate points of non-continuity or non-derivability
- Determine the limits of the function at the bounds of its definition set
- Detect the presence of infinite branches and study them
- Study variations of the function
- Determine the tangents to the curve for any stopping point, limit point or point of non-differentiability
- Graphic representation of the curve \(f\) \(\rightarrow\) synthesis
Definition set
Denominator \(\neq 0\)
The expression under \(\sqrt{}\) \(\rightarrow\) + or = 0
Log \(\rightarrow \geq 0\)
Risk of non-differentiability when \(\vert x\vert\) or n-th root used in function \(f(x)\)
Discount:
When the function is even or odd \(\rightarrow [0; +\infty[\) and symmetry
Function is periodic \(\rightarrow\) study over 1 period
Limits
$$\text{Vertical asymptotes} \rightarrow \lim_{x \to x_0\pm} f(x)=\pm \infty$$
$$\text{Horizontal asymptotes} \rightarrow \lim_{x \to \pm \infty}f(x)=l \rightarrow \text{horizontal asymptote with equation y=l}$$
$$\text{Other infinite branches } \lim_{x \to \pm \infty}f(x)=\pm \infty \rightarrow \text{asymptotic direction}$$
$$\text{Asymptotic directions} \rightarrow \text{position of } (OM) \rightarrow M(x,f(x)) \text{and direction coefficient} \frac{f(x)}{x}$$
$$\text{If} \lim_{x \to \pm \infty} \frac{f(x)}{x} \text{does not exist} \rightarrow \text{no asymptotic direction}$$< br>
$$\text{Si} \lim_{x \to \pm \infty} \frac{f(x)}{x}=\pm \infty \rightarrow \text{parabolic branch with vertical asymptotic direction}$$
$$\text{Si} \lim_{x \to \pm \infty} \frac{f(x)}{x}=0 \rightarrow \text{parabolic branch with horizontal asymptotic direction}$$
$$\text{If } \lim_{x \to \pm \infty} \frac{f(x)}{x}= a \in \mathbb{R}^* \rightarrow \lim_{x \to \pm \infty} f(x)-ax=b \in \mathbb{R} \rightarrow \text{line y=ax+b oblique asymptote}$$
$$\text{If} \lim_{x \to \pm \infty} \frac{f(x)}{x}= a \in \mathbb{R}^* \rightarrow \lim_{x \to \pm \infty} f(x)-ax=\pm \infty \rightarrow \text{parabolic branch of oblique asymptotic direction, that of y=ax.}$$
It is on or under \(y=a.x\) depending on the sign of \(f(x)-a.x\)
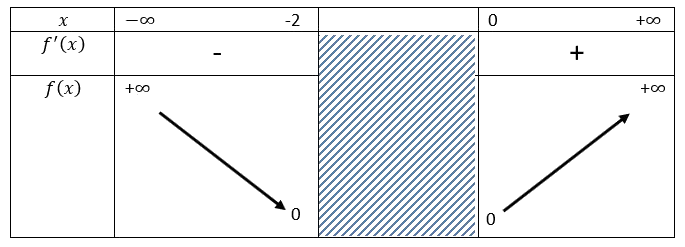
Variation table
Example: Variation table of a function defined on \(]-\infty;-2] \cap [0;+\infty[\)