Limits are a fundamental concept in mathematics that help describe how a function behaves when approaching a certain point. They make it possible to determine the approximate values to which a function tends when the independent variable approaches a certain value, even if the function never reaches this value. Limits are used to study the continuity, derivatives and integrals of a function. Limits can be finite or infinite, and it is often possible to calculate them using standard limit calculation rules. Limits are also used to study behaviors at infinity of functions, such as asymptotes.
Limits are an important part of advanced mathematical studies, and can be used to solve problems in many fields, such as physics, chemistry, finance, and engineering.
$$\lim_{x \to +\infty} x = +\infty$$ $$\lim_{x \to +\infty} e^x = +\infty$$ $$\lim_{x \to +\infty} ln(x) = +\infty$$ $$\lim_{x \to +\infty} x^n = +\infty (n \in \mathbb{N})$$ $$\lim_{x \to -\infty} x = -\infty$$ $$\lim_{x \to -\infty} e^x = 0+$$ $$\lim_{\begin{array}{cc} x \to 0 \\ x >0 \end{array}} ln(x) = -\infty$$ $$\lim_{x \to -\infty} x^n = +\infty \text{ if n even or} -\infty \text{ if n odd}$$
Addition of limits

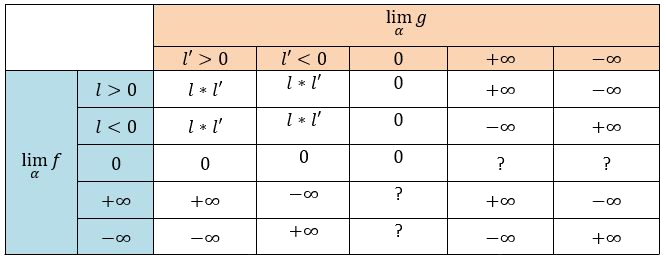
Multiplication of limits
Inversion of limits

Limit at infinity of a polynomial
Limit at infinity of the term of the + high degree, example:
$$\lim_{x \to +\infty} x^3-x^2+5x-1 = \lim_{x \to +\infty} x^3 = +\infty$$
Limit at infinity of a rational fraction
Limit at infinity of the quotient of the term of + high degree of the numerator by that of the denominator, example:
$$\lim_{x \to +\infty} \frac{-x^2+5x-1}{2-3x} = \lim_{x \to +\infty} \frac{-x^2}{- 3x} = \lim_{x \to +\infty} \frac{x}{3} = +\infty$$
$$\lim_{x \to +\infty} \frac{e^x}{x^\alpha}= +\infty (\alpha \in \mathbb{R})$$
$$\lim_{x \to -\infty} x^ne^x = 0 (n \in \mathbb{z})$$
$$\lim_{x \to +\infty} \frac{ln(x)}{x} = 0+$$
$$\lim_{\begin{array}{cc} x \to 0 \\ x >0 \end{array}} x.ln(x) = 0-$$
Null bounds and 0 bounds:
$$\lim_{x \to \alpha} f(x)=l \Longleftrightarrow \lim_{x \to \alpha} (f(x)-l)=0$$
Theorem (Rules) of comparison
We assume:
$$\forall x f(x) \leq g(x)\text{ and }\lim_{x \to \alpha} f(x)\text{ and }\lim_{x \to \alpha} g(x )\text{ exist (finite or infinite limits)}$$
So:
$$\lim_{x \to \alpha} f(x) \leq \lim_{x \to \alpha} g(x)$$
$$\text{If } f(x) < g(x)\text{ then }\lim_{x \to \alpha} f(x) \leq g(x)$$
It is assumed that both limits exist, but it is possible that one or none of the limits exist even if \(f(x) \leq g(x)\) , which leads to:
Squeeze theorem
Let \(f\),\(g\) and \(h\) be 3 functions. We assume that: \(\forall x f(x) \leq g(x) \leq h(x)\)
We also assume that:
$$\lim_{x \to \alpha} f(x)\text{ and }\lim_{x \to \alpha} h(x)\text{ exist and are equal: }\lim_{x \to \alpha } f(x)=\lim_{x \to \alpha} h(x)=l$$
Conclusion: The limit of \(g(x)\) exists when \(x \rightarrow \alpha\), and:
$$\lim_{x \to \alpha} g(x)=l$$
Application:
$$\text{Let }\lim_{x \to \alpha} g(x)=0\text{ and }\forall x \mid f(x)\mid \leq g(x)$$
Conclusion:
$$\lim_{x \to \alpha} f(x)=0$$
Special case:
$$ \text{Let }\lim_{x \to \alpha} f(x)=+\infty \text{ and }\forall x f(x) \leq g(x)$$
So:
$$\lim_{x \to \alpha} g(x)=+\infty$$
\(\rightarrow\) For \(lim=+\infty\), 1 single constable is sufficient as for \(-\infty\)
Composition of limits
$$\lim_{x \to \alpha} f(x)= \beta \text{ and } \lim_{x \to \alpha} g(x)=\gamma \rightarrow \lim_{x \to \alpha} g \circ f(x)=\gamma$$
Or:
$$\lim_{x \to \alpha} f(x)= \beta \text{ and } \lim_{x \to \alpha} g(y)=\gamma \rightarrow \lim_{x \to \alpha} g(f(x))=\gamma$$
Example
Calculate:
$$\lim_{x \to \alpha} \frac{(ln(x))^\alpha}{x^\beta } with \alpha>0 and \beta>0 and x>0$$
Denominator: \(x^\alpha = e^{\beta ln(x)} \rightarrow ln(x^n ) = n.ln(x)\)
$$\Longrightarrow \lim_{x \to +\infty} ln(x) = +\infty; \lim_{x \to +\infty} \beta.ln(x) = +\infty\text{ car }\beta>0 $$
$$\lim_{x \to +\infty} e^x = +\infty$$
So:
$$\lim_{x \to +\infty} e^{\beta lnx} = \lim_{x \to +\infty} x^\beta = +\infty$$
Numerator:
$$\lim_{x \to +\infty} ln(x) =+\infty; \lim_{x \to +\infty} y^\alpha = +\infty;\text{ so }\lim_{x \to +\infty} (ln(x))^\alpha = +\infty $$
Indeterminate form: \(\frac{\infty}{\infty}\)
Example of a limit study
Either:
$$f(x)=\frac{(ln(x))^\alpha}{x^\beta } =(\frac{ln(x)}{x^{\frac{\beta}{\ alpha}}})^\alpha$$
$$ g(x)=\frac{ln(x^1)}{x^{\frac{\beta}{\alpha}}}=\frac{ln(x^{\frac{\beta} {\alpha}.\frac{\alpha}{\beta}})}{x^{\frac{\beta}{\alpha}}}=\frac{ln((x^{\frac{\beta }{\alpha}})^{\frac{\alpha}{\beta}})}{x^{\frac{\beta}{\alpha}}}=\frac{\alpha}{\beta}. \frac{ln(x^{\frac{\beta}{\alpha}})}{x^{\frac{\beta}{\alpha}}}$$
Limit in \(+\infty\):
$$g(x)=\frac{ln(x)}{x^{\frac{\beta}{\alpha}}}$$
$$\lim_{x \to +\infty} x^{\frac{\beta}{\alpha}}=+\infty\text{ and }\lim_{y \to +\infty} \frac{ln (y)}{y}=0+\text{ (indeterminate form of reference)}$$
$$\lim_{x \to +\infty} \frac{ln(x^{\frac{\beta}{\alpha}})}{x^{\frac{\beta}{\alpha}}} =0+$$
Multiplication by \(\frac{\beta}{\alpha}>0\):
$$\lim_{x \to +\infty} g(x)=0+$$
Note:
$$f(x)=g(x)^{\alpha} \rightarrow\text{ 0+ limit of }x^{\alpha}=e^{\alpha .ln(x)}?$$
$$\lim_{x \to 0+}ln(x)=-\infty\text{ so }\lim_{x \to 0+} \alpha.ln(x)=-\infty (\alpha> 0), \lim_{y \to -\infty} e^{y} =0+$$
So: $$\lim_{x \to 0+} e^{\alpha .ln(x)}=\lim_{x \to 0+} x^{\alpha }=0+$$
Conclusion:
$$\lim_{x \to +\infty} g(x)=0+\text{ and }\lim_{x \to 0+} y^{\alpha}=0+,\text{ so }\lim_ {x \to +\infty} f(x)=\lim_{x \to +\infty} g(x)^{\alpha}=0+$$
So:
$$\forall \alpha>0, \forall \beta>0, \lim_{x \to +\infty} \frac{ln(x)^{\alpha}}{x^{\beta }}=0 +$$
Power functions “trump” logarithm functions.