Plan d’étude
Soit \(f\) : (domaine de définition \(x\), par ex : \(\mathbb{R}\)) \(\rightarrow\) (domaine de définition \(y\), par ex : \(\mathbb{R}\)), \(f(x)=\) …
- Préciser l’ensemble de définition
- Détecter & étudier les points de non-continuité ou de non-dérivabilité
- Déterminer les limites de la fonction aux bornes de son ensemble de définition
- Détecter la présence de branches infinies et les étudier
- Étudier les variations de la fonction
- Déterminer les tangentes à la courbe pour tout point d’arrêt, point limite ou point de non-dérivabilité
- Représentation graphique de la courbe \(f\) \(\rightarrow\) synthèse
Ensemble de définition
Dénominateur \(\neq 0\)
L’expression sous \(\sqrt{}\) \(\rightarrow\) + ou = 0
Log \(\rightarrow \geq 0\)
Risque de non-dérivabilité lorsque \(\vert x\vert\) ou racine n-ième utilisé dans la fonction \(f(x)\)
Réduction :
Lorsque la fonction est paire ou impaire \(\rightarrow [0; +\infty[\) et symétrie
Fonction est périodique \(\rightarrow\) étudier sur 1 période
Limites
$$\text{Asymptotes verticales} \rightarrow \lim_{x \to x_0\pm} f(x)=\pm \infty$$
$$\text{Asymptotes horizontales} \rightarrow \lim_{x \to \pm \infty}f(x)=l \rightarrow \text{asymptote horizontale d’équation y=l}$$
$$\text{Autres branches infinies } \lim_{x \to \pm \infty}f(x)=\pm \infty \rightarrow \text{direction asymptotique}$$
$$\text{Directions asymptotiques} \rightarrow \text{position de } (OM) \rightarrow M(x,f(x)) \text{et coefficient directeur} \frac{f(x)}{x}$$
$$\text{Si} \lim_{x \to \pm \infty} \frac{f(x)}{x} \text{n’existe pas} \rightarrow \text{pas de direction asymptotique}$$
$$\text{Si} \lim_{x \to \pm \infty} \frac{f(x)}{x}=\pm \infty \rightarrow \text{branche parabolique de direction asymptotique verticale}$$
$$\text{Si} \lim_{x \to \pm \infty} \frac{f(x)}{x}=0 \rightarrow \text{branche parabolique de direction asymptotique horizontale}$$
$$\text{Si } \lim_{x \to \pm \infty} \frac{f(x)}{x}= a \in \mathbb{R}^* \rightarrow \lim_{x \to \pm \infty} f(x)-ax=b \in \mathbb{R} \rightarrow \text{droite y=ax+b asymptote oblique}$$
$$\text{Si} \lim_{x \to \pm \infty} \frac{f(x)}{x}= a \in \mathbb{R}^* \rightarrow \lim_{x \to \pm \infty} f(x)-ax=\pm \infty \rightarrow \text{branche parabolique de direction asymptotique oblique, celle de y=ax.}$$
Elle est sur ou sous \(y=a.x\) suivant le signe de \(f(x)-a.x\)
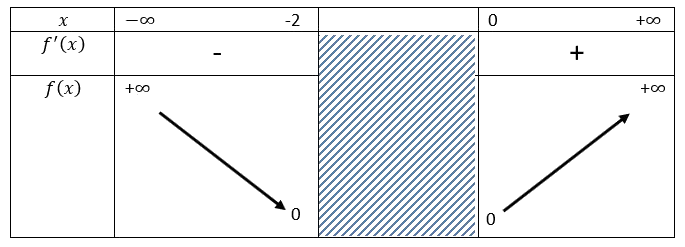
Tableau de variation
Exemple : Tableau de variation d’une fonction définie sur \(]-\infty;-2] \cap [0;+\infty[\)